Для начала вспомним формулы, которые используют при решении подобных задач: S = υ·t, υ = S : t, t = S : υ
где S – расстояние, υ – скорость движения, t – время движения.
Когда два объекта движутся равномерно с разными скоростями, то расстояние между ними за каждую единицу времени или увеличивается, или уменьшается.
Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
Движение на сближение можно разделить на два вида: встречное движение и движение вдогонку. Движение на удаление можно разделить на два вида: движение в противоположных направлениях и движение с отставанием.
Трудность для некоторых учеников заключается в том, чтобы правильно поставить «+» или «–» между скоростями при нахождении скорости сближения объектов или скорости удаления.
Рассмотрим таблицу.
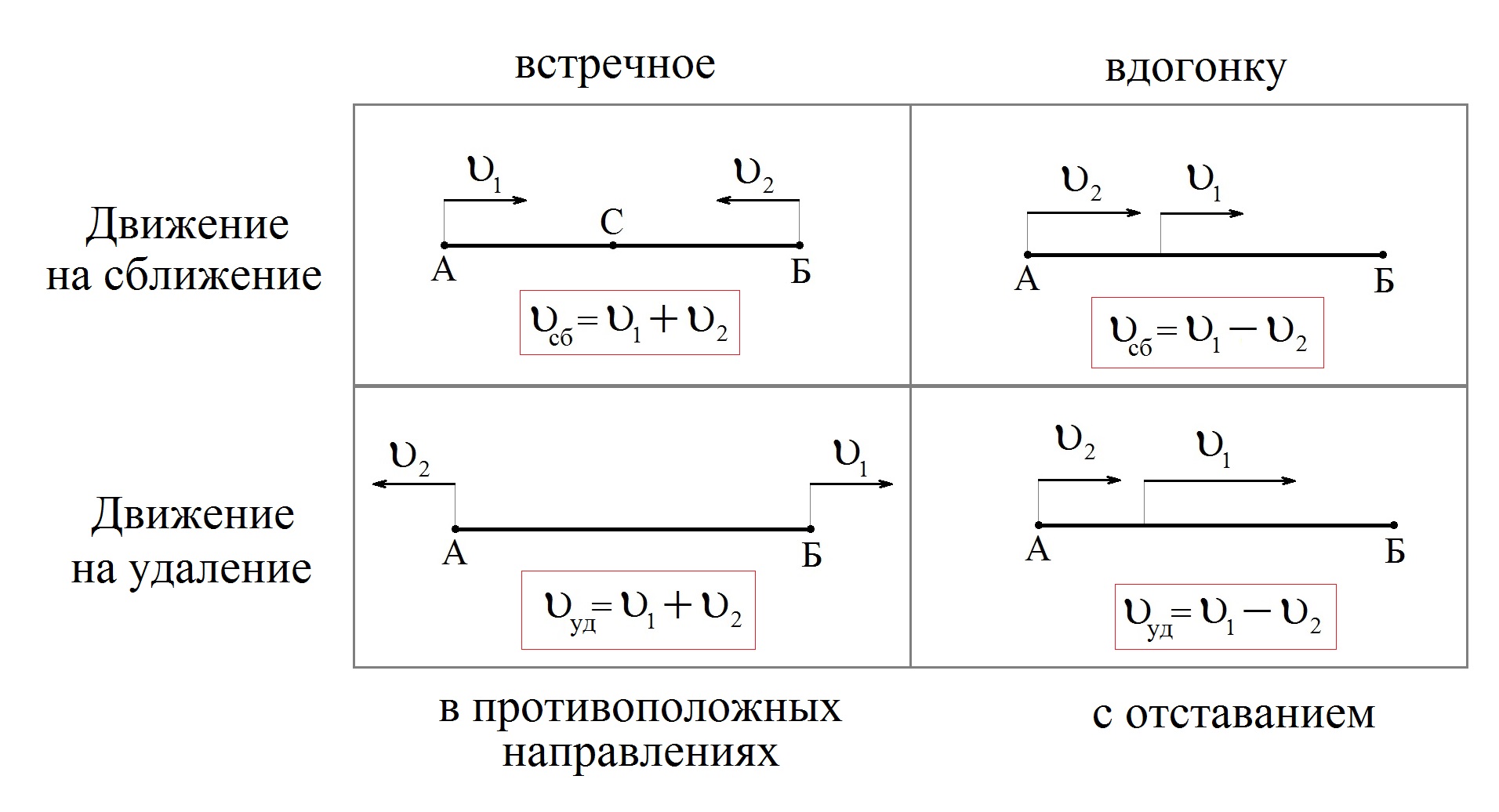
Из неё видно, что при движении объектов в противоположные стороны их скорости складываются. При движении в одну сторону – вычитаются.
Примеры решения задач.
Задача №1. Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
υ1 = 60 км/ч
υ2 = 80 км/ч
Найти υсб
Решение.
υсб = υ1 + υ2 – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υсб = 60 + 80 = 140 (км/ч)
Ответ: скорость сближения 140 км/ч.
Задача №2. Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
υ1 = 60 км/ч
υ2 = 80 км/ч
Найти υуд
Решение.
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υуд = 80 + 60 = 140 (км/ч)
Ответ: скорость удаления 140 км/ч.
Задача №3. Из одного пункта в одном направлении выехали сначала автомобиль со скоростью 60 км/ч, а затем мотоцикл со скоростью 80 км/ч. Определите скорость сближения машин.
(Видим, что здесь случай движения вдогонку, поэтому находим скорость сближения)
υав = 60 км/ч
υмот = 80 км/ч
Найти υсб
Решение.
υсб = υ1 – υ2 – скорость сближения (знак «–» так как из условия понятно, что машины движутся в одном направлении)
υсб = 80 – 60 = 20 (км/ч)
Ответ: скорость сближения 20 км/ч.
То есть название скорости – сближения или удаления – не влияют на знак между скоростями. Имеет значение только направление движения.
Рассмотрим другие задачи.
Задача № 4. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3 ч?
υ1 = 5 км/ч
υ2 = 4 км/ч
t = 3 ч
Найти S
Решение.
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υуд = 5 + 4 = 9 (км/ч)
(Пройденное расстояние находим по формуле)
S = υуд·t
S = 9·3 = 27 (км)
Ответ: через 3 ч расстояние будет 27 км.
Задача № 5. Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
S = 36 км
υ1 = 10 км/ч
υ2 = 8 км/ч
Найти t
Решение.
υсб = υ1 + υ2 – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υсб = 10 + 8 = 18 (км/ч)
(время встречи можно рассчитать по формуле)
t = S : υсб
t = 36 : 18 = 2 (ч)
Ответ: встретятся через 2 ч.
Задача №6. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70км/ч. Через сколько часов расстояние между ними будет 260 км?
υ1 = 60 км/ч
υ2 = 70 км/ч
S = 260 км
Найти t
Решение.
1 способ
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υуд = 60 + 70 = 130 (км/ч)
(Пройденное расстояние находим по формуле)
S = υуд·t ⇒ t = S : υуд
t = 260 : 130 = 2 (ч)
Ответ: через 2 ч расстояние между ними будет 260 км.
2 способ
Сделаем пояснительный рисунок:
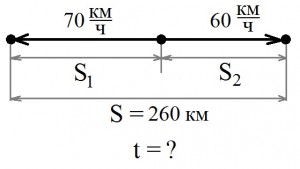
Из рисунка видно, что
1) через заданное время расстояние между поездами будет равно сумме расстояний, которые прошли каждый из поездов:
S = S1 + S2;
2) каждый из поездов ехал одинаковое время (из условия задачи), значит,
S1 =υ1· t – расстояние которое проехал 1 поезд
S2 =υ2· t – расстояние которое проехал 2 поезд
Тогда,
S = S1 + S2 = υ1· t + υ2· t = t · (υ1 + υ2) = t · υуд
t = S : (υ1 + υ2) – время за которое оба поезда проедут 260 км
t = 260 : (70 + 60) = 2 (ч)
Ответ: расстояние между поездами будет 260 км через 2 ч .
А теперь попробуйте решить задачи саомстоятельно.
1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся? (2 ч)
2. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 10 км/ч и 20 км/ч. Через сколько часов расстояние между ними будет 60 км? (2 ч)
3. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа? (9 км, 1 км)
4. Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие? (140 км, есть)
5. Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км? (28 км/ч, 2 ч)