ПРИКЛАДИ
Множення вектора на число
Відповіcти
Архіви категорії: Математика
Масштаб
Масштаб – це відношення, яке показує, у скільки разів зменшено зображення на карті (плані, кресленні, глобусі) проти його реальних розмірів на Землі. Тобто масштаб показує скільки сантиметрів на місцевості міститься в 1 см на карті.
Масштаб 1:100 000 показує, що кожному сантиметру на карті відповідає 100 000см (або 1 км) на місцевості (1 км = 100 000 см).
Чим у меншу кількість разів місцевість зменшена під час зображення її на папері, тим більшим є масштаб зображення, і навпаки.
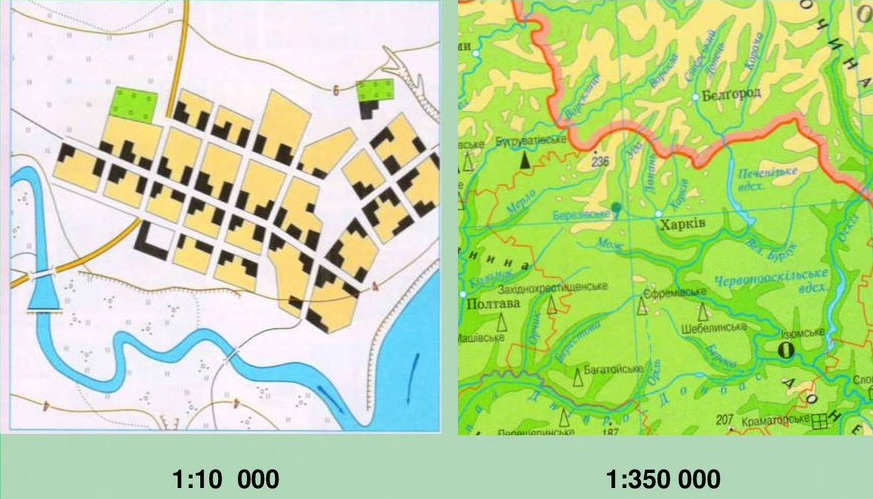
Наприклад, масштаб 1: 10 000 буде більшим, ніж масштаб 1: 350 000, тому що в першому випадку в 1 см – 100 м, а в другому – в 1 см – 3,5 км. Очевидно, що на великому масштабі місцевість буде зображена більш детально.
За масштабом карти класифікують на:
1. оглядові – масштаб більший за 1 : 1 000 000;
2. оглядово-топографічні – від 1 : 1 000 000 до 1 : 500 000;
3. дрібномасштабні – від 1 : 200 000 до 1 : 100 000;
4. середньомасштабні – від 1 : 50 000 до 1 : 25 000;
5. крупномасштабні – від 1 : 10 000 до 1 : 5000, загальногеографічні карти такого масштабу називають топографічними;
6. топографічні плани – від 1 : 2000 до 1 : 500.
За формою масштаби класифікують:
Запам’ятай! 1 км = 100 000 м; 1м = 100 см
Коротко!
ЧИСЛОВИЙ запис 1:30 000 показує, що розміри предмета на карті ЗМЕНШЕНО порівняно з реальними у 30 000 разів.
ЧИСЛОВИЙ запис 30 000:1 показує, що розміри предмета на карті ЗБІЛЬШЕНО порівняно з реальними у 30 000 разів.
Розв’язання задач
Задача 1
Масштаб карти 1:30 000, а відстань на карті між містами 45 см. Знайдіть реальну відстань між містами на місцевості.
Розв’язання.
Зрозуміло, що відстань на місцевості буде більшою за відстань на карті в 30 000 разів. Тоді 45 см × 30 000 = 1 350 000 см = 13, 5 км
Тобто ми збільшуємо відстань в 30 000 разів
Відповідь: реальна відстань між містами на місцевості 13,5 км.
Задача 2
Відстань між двома містами біля 360 км. Якою буде відстань між містами на карті, якщо масштаб цієї карти 1:300 000?
Розв’язання.
Зрозуміло, що відстань на карті буде менша за відстань на реальній місцевості в
3 000 000 разів.
360 км = 36 000 000 см.
Тоді 36 000 000 см : 3000 000 = 12 см.
Тобто ми зменшуємо реальну відстань в 3 000 000 разів
Відповідь: відстань між містами на карті 12 см.
Задача 3
Відстань між двома містами 750 км. Знайдіть масштаб карти, якщо на ній відстань між цими містами 15 см.
Розв’язання.
750 км = 75 000 000 см
Оскільки масштаб показує у скільки разів зменшено зображення на карті в порівнянні з його реальними розмірами на місцевості, тоді
75 000 000 см : 15 см = 5 000 000.
Відповідь: масштаб карти 1:5 000 000.
Прості рівняння
Рівняння – це рівність, яка містить невідоме число (букву), значення якого треба знайти, щоб рівність була правильною.
Корінь рівняння – це число, яке при підстановці його замість букви перетворює рівняння на правильну числову рівність. Розв’язати рівняння – це означає знайти всі його корені або переконатися, що їх взагалі немає.
Додавання
Як знайти невідомий доданок? Треба від суми відняти відомий доданок.
x + 3 = 5x = 5 – 3x = 2 |
4 + x = 6x = 6 – 4x = 2 |
Віднімання
Як знайти невідоме зменьшувальне? Треба до різниці додати від’ємник.
y – 15 = 10
y = 10 + 15
y = 25
Як знайти невідомий від’ємник? Треба від зменьшувального відняти різницю.
10 – b = 6
b = 10 – 6
b = 4
Множення
Як знайти невідомий множник? Треба добуток поділити на відомий множник.
c × 3 = 15с = 15 : 3с = 5 |
4 × с = 16с = 16 : 4с = 4 |
Ділення
Як знайти невідоме ділене? Треба дільник помножити на частку.
x : 3 = 4
x = 3 × 4
x = 12
Як знайти невідомий дільник? Треба ділене поділити на частку.
36 : d = 4
d = 36 : 4
d = 9
Задачи на сближение и удаление
Для начала вспомним формулы, которые используют при решении подобных задач: S = υ·t, υ = S : t, t = S : υ
где S – расстояние, υ – скорость движения, t – время движения.
Когда два объекта движутся равномерно с разными скоростями, то расстояние между ними за каждую единицу времени или увеличивается, или уменьшается.
Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
Движение на сближение можно разделить на два вида: встречное движение и движение вдогонку. Движение на удаление можно разделить на два вида: движение в противоположных направлениях и движение с отставанием.
Трудность для некоторых учеников заключается в том, чтобы правильно поставить «+» или «–» между скоростями при нахождении скорости сближения объектов или скорости удаления.
Рассмотрим таблицу.
Из неё видно, что при движении объектов в противоположные стороны их скорости складываются. При движении в одну сторону – вычитаются.
Примеры решения задач.
Задача №1. Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
υ1 = 60 км/ч
υ2 = 80 км/ч
Найти υсб
Решение.
υсб = υ1 + υ2 – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υсб = 60 + 80 = 140 (км/ч)
Ответ: скорость сближения 140 км/ч.
Задача №2. Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
υ1 = 60 км/ч
υ2 = 80 км/ч
Найти υуд
Решение.
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υуд = 80 + 60 = 140 (км/ч)
Ответ: скорость удаления 140 км/ч.
Задача №3. Из одного пункта в одном направлении выехали сначала автомобиль со скоростью 60 км/ч, а затем мотоцикл со скоростью 80 км/ч. Определите скорость сближения машин.
(Видим, что здесь случай движения вдогонку, поэтому находим скорость сближения)
υав = 60 км/ч
υмот = 80 км/ч
Найти υсб
Решение.
υсб = υ1 – υ2 – скорость сближения (знак «–» так как из условия понятно, что машины движутся в одном направлении)
υсб = 80 – 60 = 20 (км/ч)
Ответ: скорость сближения 20 км/ч.
То есть название скорости – сближения или удаления – не влияют на знак между скоростями. Имеет значение только направление движения.
Рассмотрим другие задачи.
Задача № 4. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3 ч?
υ1 = 5 км/ч
υ2 = 4 км/ч
t = 3 ч
Найти S
Решение.
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υуд = 5 + 4 = 9 (км/ч)
(Пройденное расстояние находим по формуле)
S = υуд·t
S = 9·3 = 27 (км)
Ответ: через 3 ч расстояние будет 27 км.
Задача № 5. Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
S = 36 км
υ1 = 10 км/ч
υ2 = 8 км/ч
Найти t
Решение.
υсб = υ1 + υ2 – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υсб = 10 + 8 = 18 (км/ч)
(время встречи можно рассчитать по формуле)
t = S : υсб
t = 36 : 18 = 2 (ч)
Ответ: встретятся через 2 ч.
Задача №6. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70км/ч. Через сколько часов расстояние между ними будет 260 км?
υ1 = 60 км/ч
υ2 = 70 км/ч
S = 260 км
Найти t
Решение.
1 способ
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υуд = 60 + 70 = 130 (км/ч)
(Пройденное расстояние находим по формуле)
S = υуд·t ⇒ t = S : υуд
t = 260 : 130 = 2 (ч)
Ответ: через 2 ч расстояние между ними будет 260 км.
2 способ
Сделаем пояснительный рисунок:
Из рисунка видно, что
1) через заданное время расстояние между поездами будет равно сумме расстояний, которые прошли каждый из поездов:
S = S1 + S2;
2) каждый из поездов ехал одинаковое время (из условия задачи), значит,
S1 =υ1· t – расстояние которое проехал 1 поезд
S2 =υ2· t – расстояние которое проехал 2 поезд
Тогда,
S = S1 + S2 = υ1· t + υ2· t = t · (υ1 + υ2) = t · υуд
t = S : (υ1 + υ2) – время за которое оба поезда проедут 260 км
t = 260 : (70 + 60) = 2 (ч)
Ответ: расстояние между поездами будет 260 км через 2 ч .
А теперь попробуйте решить задачи саомстоятельно.
1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся? (2 ч)
2. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 10 км/ч и 20 км/ч. Через сколько часов расстояние между ними будет 60 км? (2 ч)
3. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа? (9 км, 1 км)
4. Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие? (140 км, есть)
5. Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км? (28 км/ч, 2 ч)
Вектори. Координати векторів
У робочих зошитах виконаємо вправи за підручником: Геометрія 9 клас, (А.П.Єршова та ін.) № 468, 471, 472, 475. Спробуйте розв’язати ці вправи самостійно, а потім звіритися із “дошкою”.
ДЗ: №№462, 466, 467, 473, 479
Початкові відомості про вектори
Вам вже знайомі деякі фізичні величини (сила, переміщення, швидкість та ін), які характеризуються не тільки числовим значенням, але й напрямом.
Наприклад, автомобіль рухається зі швидкістю 80 км/год. Але це неповна інформація про рух тіла, іноді дуже важливо КУДИ саме рухається автомобіль, тобто вказати напрям його руху. Або інший приклад. На автомобіль діє сила 150 Н. Як буде рухатися автомобіль? На це питання неможна дати відповідь, доки не буде вказано напрям дії сили. Якщо сила діє горизонтально, автомобіль теж буде рухатися горизонтально. У зв’язку з цим зрозуміло, що деякі фізичні величини зручно зображати напрямленими відрізками.
Напрямлений відрізок називається вектором.
Напрямок вектора визначається зазначенням його початку та кінця. На креслені напрям вектора відмічають стрілкою.
Для позначення векторів користуються малими латинськими літерами a, b, .. – 
Також можна позначати вектор зазначенням його початку та кінця 
,
де А – початок вектора, В – кінець вектора
Довжина (модуль) вектора – це довжина відрізка АВ, який зображує вектор.
Довжину вектора позначають так: 
Основні означення
Нульовий вектор – це вектор кінець якого співпадає з його початком.
На рисунках такий вектор зображається точкою і позначають Ō. Модуль нульового вектора дорівнює нулю, а його напрям не визначений.
Колінеарні вектори – це вектори, що лежать на одній прямій або на паралельних прямих. Нульовий вектор вважається колінеарним будь-якому вектору.
Рівні вектори – це вектори, які суміщаються паралельним переносом.
Основні властивості та ознаки рівних векторів:
1. Рівні вектори співнаправлені та мають рівні довжини;
2. Якщо вектори співнапрямлені та мають рівні довжини, то вони рівні;
3. Від будь-якої точки можна відкласти вектор, рівний даному, але тільки один.
Колінеарні вектори – це вектори, що лежать на одній прямій або на паралельних прямих. Нульовий вектор вважається колінеарним будь-якому вектору.
Координати вектора
Спочатку повторимо теоретичний матеріал.
Завдання: в зошитах з теорії зробити конспект з теми, проілюструвати задачами №№448, 452, 458, 460, 455 (за підручником Геометрія 9 клас, (А.П.Єршова та ін))
Розв’язання задач
ДЗ: №№ 454, 461, 463.
Вектори. Координати векторів
На останньому уроці ми розпочали вивчення теми “Вектори. Координати векторів.”
Продовжуємо розв’язувати задачі з цієї теми.
У робочих зошитах виконаємо вправи за підручником: Геометрія 9 клас, (А.П.Єршова та ін.) № 468, 471, 472, 475. Спробуйте розв’язати ці вправи самостійно, а потім звіритися із “дошкою”.
ДЗ: №№462, 466, 467, 473, 479
Признаки делимости на натуральные числа
Признак делимости на 2. Число делится на 2, если его последняя цифра – чётное число.
Числа, делящиеся на два, называются чётными, не делящиеся на два – нечётными. Ноль – чётное число.
Признак делимости на 4. Число делится на 4, если две его последние цифры – нули или образуют число, которое делится на 4.
Признак делимости на 8. Число делится на 8, если три его последние цифры – нули или образуют число, которое делится на 8.
Признаки делимости на 3 и 9. Число делится на 3, если его сумма цифр делится на 3. Число делится на 9, если его сумма цифр делится на 9.
Признак делимости на 6. Число делится на 6, если оно делится на 2 и на 3.
Признак делимости на 5. Число делится на 5, если его последняя цифра – ноль или 5.
Признак делимости на 7. Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7).
Признак делимости на 11. На 11 делятся только те числа, у которых сумма цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, делящееся на 11.
Признак делимости на 13. Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 · 5) = 104 делится на 13).
Признак делимости на 17. Делимость числа на 17 зависит от соотношения между цифрами числа без его последней цифры и этой последней цифрой. Натуральное число делится на 17, если разность — это число без его последней цифры минус его последняя цифра, умноженная на 5, — делится на 17.
Признак делимости на 25. Число делится на 25, если две его последние цифры – нули или образуют число, которое делится на 25.
Признак делимости на 10. Число делится на 10, если его последняя цифра – ноль.
Признак делимости на 100. Число делится на 100, если две его последние цифры – нули.
Признак делимости на 1000. Число делится на 1000, если три его последние цифры – нули.
Загадка Ейнштейна
Загадка Ейнштейна – відома логічна задача, яка за легендою створена Альбертом Ейнштейном в роки його дитинства. Також існує думка, що вона використовувалася Ейнштейном для перевірки кандидатів в асистенти на здатність до логічного мислення. Іноді автором головоломки називають Льюїса Керролла. Тим не менше, немає ніяких доказів того, що завдання придумав Ейнштейн або Керролл. Більш того, в наведеній нижче умові задачі згадуються марки сигарет, наприклад Kool (англ.), які не існували за життя Керролла і за часів дитинства Ейнштейна. Але загадка цікава для тих, хто любить розв’язувати різні логічні задачки. Нижче наведено перший відомий варіант головоломки, яку було опубліковано в журналі Life 17 грудня 1962 року.
На вулиці стоять п’ять будинків.
1. Англієць живе в червоному будинку.
2. У іспанця є собака.
3. У зеленому будинку п’ють каву.
4. Українець п’є чай.
5. Зелений будинок стоїть одразу праворуч від білого дому.
6. Той, хто курить Old Gold, розводить равликів.
7. У жовтому будинку курять Kool.
8. У центральному будинку п’ють молоко.
9. Норвежець живе в першому будинку.
10. Сусід того, хто курить Chesterfield, тримає лисицю.
11. У будинку по сусідству з тим, в якому тримають коня, курять Kool.
12. Той, хто курить Lucky Strike, п’є апельсиновий сік.
13. Японець курить Parliament.
14. Норвежець живе поруч з синім будинком.
Хто п’є воду? Хто тримає зебру?
З метою уточнення слід додати, що кожен з п’яти будинків має свій колір, а їх жителі – різних національностей, володіють різними тваринами, п’ють різні напої і курять різні марки американських сигарет. Ще одне зауваження: в твердженні 6 “праворуч” означає справа щодо вас.
Якщо задача вам сподобалась, тоді запропоную ще одну із книги “Удивительный мир чисел. Математические головоломки и задачи для любознательных” Кордемский Б.А., Ахадов А.А.
На одній з вулиць дачного селища всього п’ять будинків. Вони пофарбовані в різні кольори, і в них живуть родини поета, письменника, критика, журналіста і редактора. У будинку кожної сім’ї живе улюблена пташка. Глава сім’ї отримує на сніданок улюблений їм напій, після чого відправляється в місто, користуючись улюбленим способом пересування. Відомо що:
1. Поет користується велосипедом.
2. Редактор живе в червоному будинку.
3. Критик живе в крайньому будинку зліва, поруч розташований блакитний будинок.
4. Той, хто їздить на мотоциклі, живе в середньому будинку.
5. Той, хто живе в зеленому будинку, розташованому поруч з білим, праворуч від нього, завжди відправляється в місто пішки.
6. У будинку, де живе снігур, на сніданок завжди буває молоко.
7. Той хто на сніданок отримує какао, живе в будинку, сусідньому з тим будинком, де живе синиця.
8. У жовтому будинку на сніданок подають чай.
9. Який мешкав у сусідньому з любителем канарок вранці п’є чай.
10. Письменник п’є тільки каву.
11. Той, хто їздить на своєму автомобілі, любить пити томатний сік.
12. У будинку журналіста живе папужка.
Питання: У кого живе сорока?
Распределительное свойство умножения
Распределительное свойство умножения относительно сложения
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
или так:
(b + c) a = ab + ac
В ответе буквы записываются в алфавитном порядке.
Распределительное свойство умножения выполняется для трёх и более слагаемых.
Например, a(b + c + d +f) = ab + ac + ad + af
Распределительное свойство умножения относительно вычитания
Чтобы число умножить на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое и из первого произведения вычесть второе.
В буквенном виде это свойство записывают так:
a(b – c) = ab – ac
или так:
(b – c) a = ab – ac
Примеры:
4 (a + 2) = 4a + 4·2 = 4a +8
-6a(3b – 5c – d) = -18 ab + 30 ac + 6 ad
(3x + 4y +5z)2 = 2·3x + 2·4y + 2·5z = 6x + 8y +10z
3b (4b + c) = 3b·4b + 3b·c = 12b2 + 3b·c
Задания
Раскрыть скобки
3 (a + 5)
8 (5 – x)
15 (c + d)
-20 (f – g)
(a + b) 4
-14a(a + b)
(x – y) 18
2a (3 + 2b)
20 (4a – 5)
(3c + 5d)·(-14)
(2x + 3y) 8x
(3m + 4n – 7p) ·(-6)
-5a (b + 3c – 6d + 2f)
(2a – 5b + 3 c) 12
Упростите выражение
12 a + 13 a
39 b – b
d + 27 d
36 d – 19 d + 23 d
46 a + 54 a – a – 2 a
23 m – 14 m +48
56 b + 14 b – 70 b
37 x – 17 x + 34 x – 54 x + 100
12 a + 6 b
24 x – 8 y
18 a + a +12 a
18 a + 6 b +12 c
14 c + 7 c + 9
69 p – 13 p + 37
14 a – 8 a + 45 a + a
15 a + 5 b + 20 c – 10 d
Решите уравнения
15x + 26 x – 14 = 68
48 x – 19 x = 145
(((12x + 3x) – 5x) – 2x) + 10 x = 54
Розподільна властивість множення від storybook